Prawo Ohma dla całego łańcucha i jego odcinka: możliwości zapisania wzoru, opisu i objaśnienia

Profesjonalny elektryk czy elektronik nie ma możliwości ominięcia prawa Ohma w swojej działalności, rozwiązując wszelkie problemy związane z konfiguracją, regulacją i naprawą obwodów elektronicznych i elektrycznych.

Właściwie każdy musi zrozumieć to prawo. Ponieważ każdy ma do czynienia z prądem na co dzień.

I chociaż prawo niemieckiego fizyka Ohma jest zapisane w programie nauczania w szkole średniej, w praktyce nie zawsze jest ono studiowane w odpowiednim czasie. Dlatego w naszym materiale rozważymy tak istotny temat na całe życie i zrozumiemy opcje napisania formuły.

Pojedyncza sekcja i kompletny obwód elektryczny

Rozważając obwód elektryczny z punktu widzenia zastosowania prawa Ohma do obwodu, należy zwrócić uwagę na dwie możliwe opcje obliczeń: dla oddzielnej sekcji i dla pełnoprawnego obwodu.

Obliczanie prądu odcinka obwodu elektrycznego

Za część obwodu elektrycznego uważa się z reguły część obwodu, która wyklucza źródło pola elektromagnetycznego, ponieważ ma dodatkowy opór wewnętrzny.

Dlatego wzór obliczeniowy w tym przypadku wygląda prosto:

Ja = U/R,

Gdzie odpowiednio:

• I – siła prądu;
• U - zastosowane napięcie;
• R - opór.

Interpretacja wzoru jest prosta - prąd przepływający przez pewien odcinek obwodu jest proporcjonalny do przyłożonego do niego napięcia, a rezystancja jest odwrotnie proporcjonalna.

Tzw. graficzna „stokrotka”, poprzez którą przedstawiony jest cały zestaw odmian sformułowań opartych na prawie Ohma. Wygodne narzędzie do przechowywania w kieszeni: sektor „P” - formuły mocy; sektor „U” - wzory na napięcie; sektor „I” - aktualne formuły; sektor „R” - formuły oporu

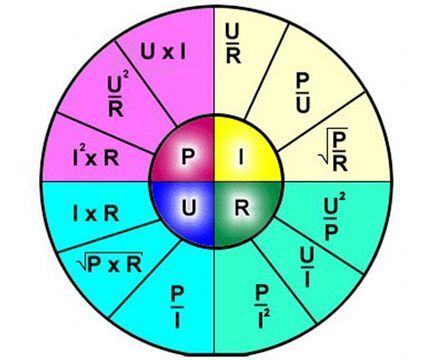
Zatem wzór wyraźnie opisuje zależność przepływu prądu przez oddzielną sekcję obwodu elektrycznego w stosunku do pewnych wartości napięcia i rezystancji.

Wzór jest wygodny w użyciu na przykład przy obliczaniu parametrów rezystancji, którą należy wlutować w obwód, jeśli podane jest napięcie i prąd.

Prawo Ohma i dwie konsekwencje, które musi znać każdy zawodowy inżynier elektromechanik, inżynier elektryk, elektronik i każdy, kto zajmuje się obsługą obwodów elektrycznych. Od lewej do prawej: 1 - określenie prądu; 2 - określenie rezystancji; 3 - definicja napięcia, gdzie I - prąd, U - napięcie, R - rezystancja

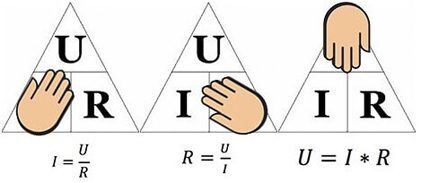
Powyższy rysunek pomoże określić na przykład prąd przepływający przez rezystancję 10 omów, do której przykładane jest napięcie 12 woltów. Podstawiając wartości, znajdujemy – I = 12 / 10 = 1,2 ampera.

W podobny sposób rozwiązuje się problemy ze znalezieniem rezystancji (gdy znany jest prąd i napięcie) lub napięcia (gdy znane jest napięcie i prąd).

Dzięki temu zawsze możesz wybrać wymagane napięcie robocze, wymagane natężenie prądu i optymalny element rezystancyjny.

Proponowany do stosowania wzór nie wymaga uwzględnienia parametrów źródła napięcia.Natomiast obwód zawierający np. akumulator będzie obliczany według innego wzoru. Na schemacie: A – włączenie amperomierza; V – włącz woltomierz.

Nawiasem mówiąc, przewody łączące dowolnego obwodu są rezystancjami. Wielkość obciążenia, jakie muszą wytrzymać, zależy od napięcia.

W związku z tym, ponownie korzystając z prawa Ohma, możliwe staje się dokładne dobranie wymaganego przekroju przewodu, w zależności od materiału rdzenia.

Na naszej stronie internetowej znajdziesz szczegółowe instrukcje obliczenia przekroju kabla pod względem mocy i prądu.

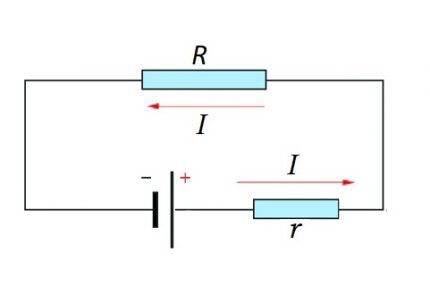
Opcja obliczeń dla całego łańcucha

Kompletny obwód składa się z sekcji (sekcji), a także źródła pola elektromagnetycznego. Oznacza to, że rezystancja wewnętrzna źródła pola elektromagnetycznego jest dodawana do istniejącej składowej rezystancyjnej sekcji obwodu.

Dlatego logiczne jest nieznaczne zmodyfikowanie powyższej formuły:

ja = U / (R + r)

Oczywiście wartość rezystancji wewnętrznej pola elektromagnetycznego w prawie Ohma dla całego obwodu elektrycznego można uznać za pomijalną, chociaż wartość tej rezystancji w dużej mierze zależy od struktury źródła pola elektromagnetycznego.

Jednak przy obliczaniu złożonych obwodów elektronicznych, obwodów elektrycznych z wieloma przewodnikami, ważnym czynnikiem jest obecność dodatkowego oporu.

Do obliczeń w warunkach kompletnego obwodu elektrycznego zawsze brana jest pod uwagę wartość rezystancji źródła pola elektromagnetycznego. Wartość ta jest sumowana z rezystancją samego obwodu elektrycznego. Na schemacie: I - przepływ prądu; R – zewnętrzny element rezystancyjny; r jest współczynnikiem oporu pola elektromagnetycznego (źródła energii)

Zarówno w przypadku odcinka obwodu, jak i całego obwodu należy wziąć pod uwagę moment naturalny - zastosowanie prądu stałego lub zmiennego.

Jeśli powyższe punkty, charakterystyczne dla prawa Ohma, rozpatrzyć z punktu widzenia wykorzystania prądu stałego, to w przypadku prądu przemiennego wszystko wygląda nieco inaczej.

Rozważenie wpływu prawa na wielkość zmienną

Pojęcie „oporu” na warunki przepływu prądu przemiennego należy traktować bardziej jak pojęcie „impedancji”. Odnosi się to do kombinacji obciążenia rezystancyjnego (Ra) i obciążenia rezystorem biernym (Rr).

Zjawiska takie spowodowane są parametrami elementów indukcyjnych i prawami przełączania w odniesieniu do zmiennej wartości napięcia – sinusoidalnej wartości prądu.

Jest to obwód zastępczy obwodu elektrycznego prądu przemiennego do obliczeń przy użyciu formuł opartych na zasadach prawa Ohma: R - składnik rezystancyjny; C jest składnikiem pojemnościowym; L – element indukcyjny; Pole elektromagnetyczne jest źródłem energii; Ja - przepływ prądu

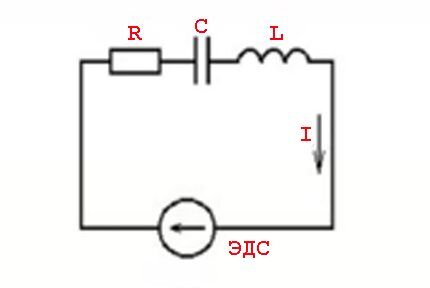
Innymi słowy, występuje efekt wyprzedzenia (opóźnienia) wartości prądu od wartości napięcia, czemu towarzyszy pojawienie się mocy czynnej (rezystancyjnej) i biernej (indukcyjnej lub pojemnościowej).

Zjawiska takie oblicza się za pomocą wzoru:

Z=U/I Lub Z = R + J * (X_L -X_C)

Gdzie: Z – impedancja; R – obciążenie czynne; X_L , X_C – obciążenie indukcyjne i pojemnościowe; J - współczynnik.

Szeregowe i równoległe łączenie elementów

Dla elementów obwodu elektrycznego (odcinka obwodu) punktem charakterystycznym jest połączenie szeregowe lub równoległe.

W związku z tym każdemu rodzajowi połączenia towarzyszy inny wzór przepływu prądu i zasilania napięciem.W związku z tym prawo Ohma jest również stosowane w różny sposób, w zależności od opcji uwzględnienia elementów.

Obwód połączonych szeregowo elementów rezystancyjnych

W odniesieniu do połączenia szeregowego (odcinka obwodu składającego się z dwóch elementów) stosuje się następujące sformułowanie:

• ja = ja₁ = ja₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Sformułowanie to wyraźnie pokazuje, że niezależnie od liczby elementów rezystancyjnych połączonych szeregowo, prąd płynący przez odcinek obwodu nie zmienia wartości.

Połączenie elementów rezystancyjnych w odcinku obwodu szeregowo ze sobą. Ta opcja ma własne prawo obliczeniowe. Na schemacie: I, I1, I2 - przepływ prądu; R1, R2 - elementy rezystancyjne; U, U1, U2 - przyłożone napięcie

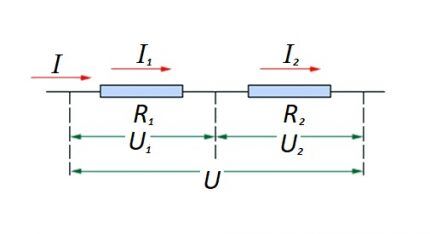
Wielkość napięcia przyłożonego do skutecznych elementów rezystancyjnych obwodu jest sumą i sumuje wartość źródła emf.

W takim przypadku napięcie na każdym pojedynczym elemencie jest równe: Ux = I * Rx.

Całkowitą rezystancję należy uznać za sumę wartości wszystkich elementów rezystancyjnych w obwodzie.

Obwód równolegle połączonych elementów rezystancyjnych

W przypadku równoległego połączenia elementów rezystancyjnych za sprawiedliwe w odniesieniu do prawa niemieckiego fizyka Ohma uważa się następujące sformułowanie:

• ja = ja₁ +ja₂ … ;
• U = U₁ = U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Nie wyklucza się opcji tworzenia odcinków obwodu typu „mieszanego”, gdy stosowane są połączenia równoległe i szeregowe.

Połączenie elementów rezystancyjnych na odcinku obwodu równolegle do siebie. W przypadku tej opcji stosowane jest inne prawo obliczeniowe. Na schemacie: I, I1, I2 - przepływ prądu; R1, R2 - elementy rezystancyjne; U to dostarczane napięcie; A, B - punkty wejścia/wyjścia

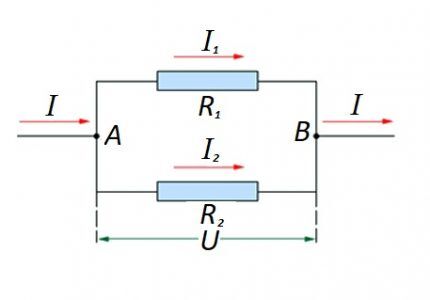
W przypadku takich opcji obliczenia zwykle przeprowadza się poprzez wstępne obliczenie rezystancji połączenia równoległego. Następnie do otrzymanego wyniku dodawana jest wartość rezystora połączonego szeregowo.

Całkowe i różniczkowe formy prawa

Wszystkie powyższe punkty wraz z obliczeniami mają zastosowanie do warunków, w których w obwodach elektrycznych stosowane są przewodniki o, że tak powiem, „jednorodnej” strukturze.

Tymczasem w praktyce często mamy do czynienia z konstrukcją schematów, gdzie struktura przewodów zmienia się w różnych przekrojach. Na przykład stosuje się druty o większym przekroju lub odwrotnie, mniejszym, wykonane z różnych materiałów.

Aby uwzględnić takie różnice, istnieje odmiana tak zwanego „prawa różniczkowo-całkowego Ohma”. W przypadku nieskończenie małego przewodnika poziom gęstości prądu jest obliczany w zależności od wartości napięcia i przewodności.

Do obliczeń różnicowych stosuje się następujący wzór: J = ό * E

Odpowiednio do obliczenia całkowego wzór wygląda następująco: I * R = φ1 – φ2 + έ

Przykłady te są jednak raczej bliższe szkole wyższej matematyki i tak naprawdę nie są stosowane w rzeczywistej praktyce prostego elektryka.

Wnioski i przydatne wideo na ten temat

Szczegółowa analiza prawa Ohma w poniższym filmie pomoże w końcu utrwalić wiedzę w tym kierunku.

Unikalna lekcja wideo jakościowo wzmacnia teoretyczną prezentację pisemną:

Praca elektryka czy elektronika nierozerwalnie wiąże się z momentami, w których rzeczywiście trzeba przestrzegać prawa Georga Ohma w działaniu. To pewnego rodzaju truizmy, które powinien znać każdy profesjonalista.

Nie jest wymagana rozległa wiedza na ten temat – wystarczy poznać trzy główne warianty sformułowania, aby z powodzeniem zastosować je w praktyce.

Chcesz uzupełnić powyższy materiał o wartościowe uwagi lub wyrazić swoją opinię? Komentarze prosimy zamieszczać w bloku pod artykułem. Jeśli masz jakieś pytania, nie wahaj się zapytać naszych ekspertów.